Vison Transformer系列文章解读（一）

引言

x x x

1. Transformer快速回顾

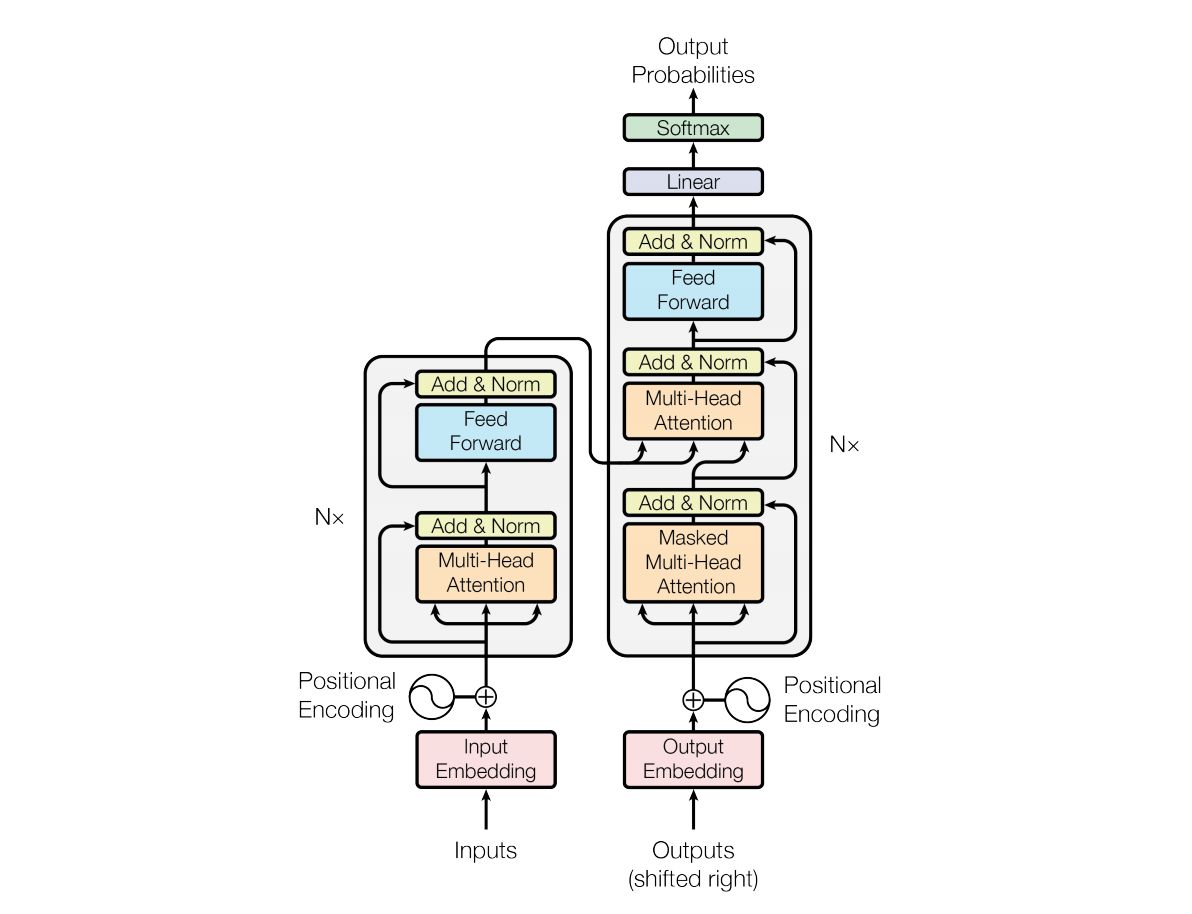
我们先来简单而快速的回顾一下Transformer的构成。和串处理数据的Seq2Seq模型不同，Transformer在处理序列数据时，能够做到并行，这也使得Transformer在Seq2Seq模型中快速脱颖而出。

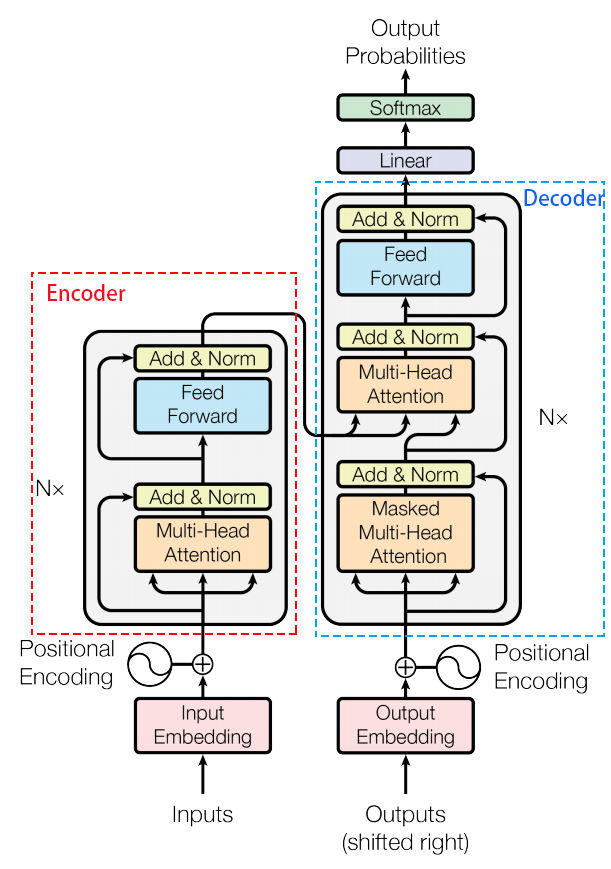
1.1 Encoder侧输入数据详情

假设上图中的Encoder侧的inputs是一个[$ x^1, x^2, x^3, x^4$]的序列，该序列长度为4，而每个时间点上的输入数据$ x^i \in \R^{d_{model}}$，这样一个shape为[seq_len, $ d_{model}$]的tensor进入到input Embedding中，通过乘以三种不同的可学习权重矩阵$ W_q, W_k, W_v$，其中$W_q \in \mathbb{R}^{d_{model}\times dimension}, W_k \in \R^{d_{model}\times dimension}, W_v \in \R^{d_{model}\times dimension}$，然后就可以将原来$d_{model}$维的序列数据转换转换为$dimension $维。值得注意的是，我们在实现transformer的Encoder过程中，为了极大程度的使用矩阵并行计算的优点，我们会将$W_q,W_k, W_v$矩阵和在一起进行统一计算，得到结果后，再将tensor进行split。同样的道理，当我们会用到multi-head的attention时，（假如我们有k个头）我们也不会分离的做一次，在去继续做k-1次，而是统一把所有头的参数集中放在一起，统一经过矩阵运算得到结果后，再去把结果split成k个头。就这样，我们可以把输入数据进行初次的Linear Layer变换。但这样变换完成后，序列数据中的先后顺序和空间位置信息被丢失了，即把输入数据[$x^1, x^2, x^3, x^4$]打乱顺序也能得到一样的结果，但很明显，这样的位置不敏感是不正确的，因此，我们下面需要为embedding添加位置编码信息进去。

1.2 Encoder侧位置编码

对于位置的编码方式，我们可以用绝对位置编码，相对位置编码和可学习的位置编码。

绝对位置编码
$$
PositionEmbedding(pos, 2i) = sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) \
PositionEmbedding(pos, 2i+1) = cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}})
$$
上式中$pos \in [0, seqlen)$，表示token在序列中的位置；$i\in[0, d_{model})$，表示embedding的各个维度的索引。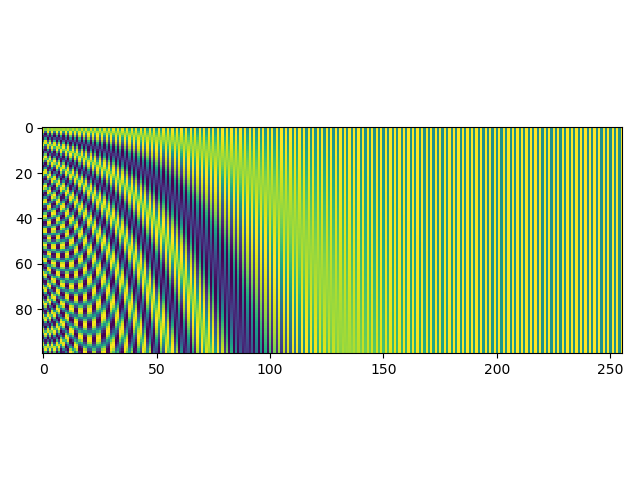
相对位置编码

相对位置并没有完整建模每个输入的位置信息，而是在算Attention的时候考虑当前位置与被Attention的位置的相对距离，由于自然语言一般更依赖于相对位置，所以相对位置编码通常也有着优秀的表现。相对位置编码也有好几类，分为bias偏置类和contextual上下文类等几种。
- contextual上下文型相对位置
  $$
  z_i = \sum_{j=1}^n \alpha_{ij}(x_jW^V + p_{ij}^V)\
  \alpha_{ij} = \frac{(x_i W^Q+p_{ij}^Q)(x_j W^K+p_{ij}^K)^T}{\sqrt{d_z}}
  $$
  上式中，$z_i$表示token第$i$个位置的输出向量，$\alpha_{ij}$表示token第i个位置和第j个位置的attention，$x_j\in\R^{d_{model}}$是第j个位置的token的向量值，$W^V\in \R^{d_{model}\times dimension}$表示将输入embedding转换为value的可学习权重矩阵。$p_{ij}^V \in \R^{dimension}$表示value侧的相对位置值向量，它是指第i个token和第j个token的相对位置clip(i-j, max_k)。
- bias偏置型相对位置编码
  $$
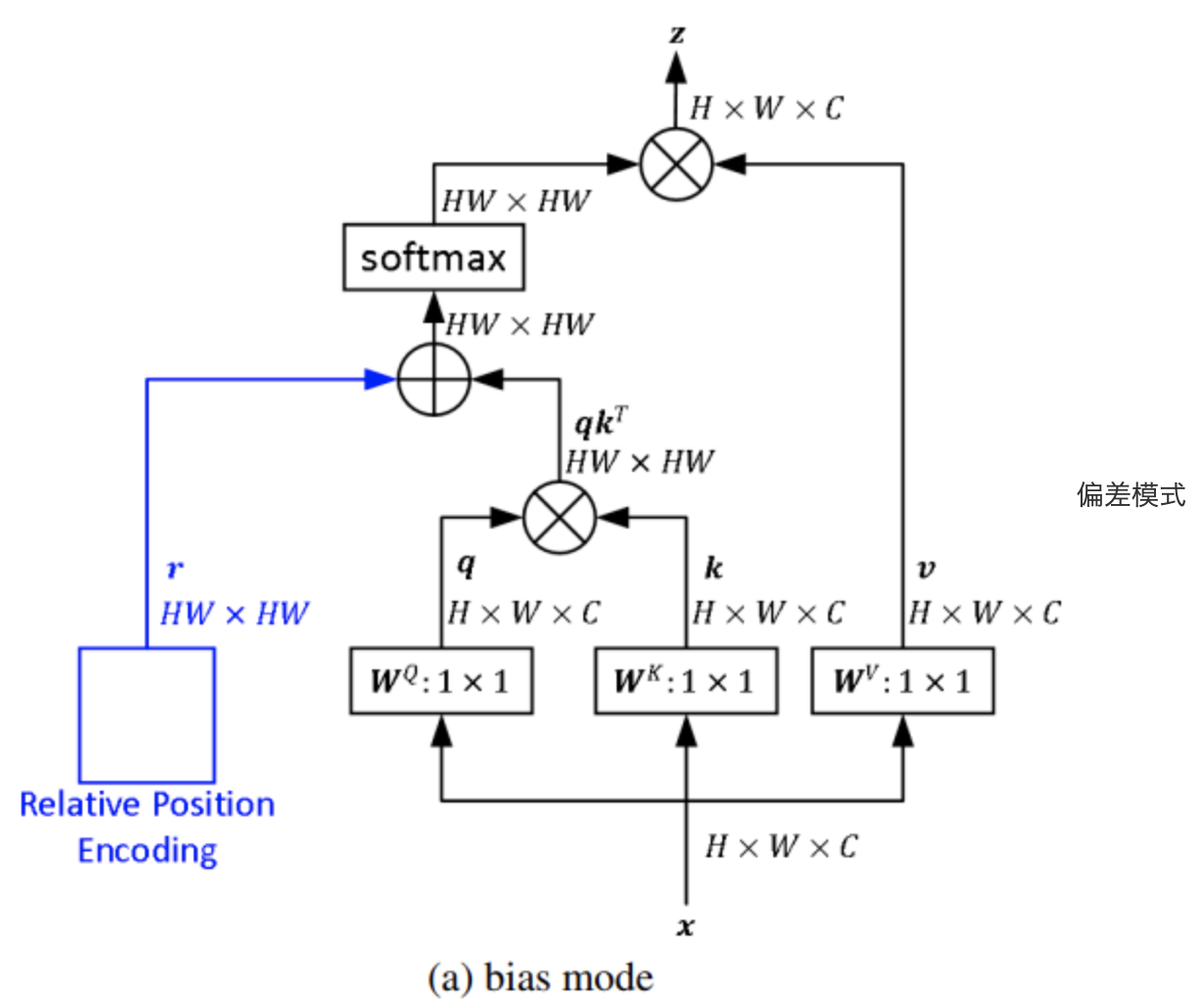
  \alpha_{ij}=\frac{(x_i W^Q)(x_j W^K)^T + b_{ij}}{\sqrt{d_z}}
  $$
  上式中，相对位置编码和输入完全无关，是单独计算出attention矩阵后，再将相对位置编码加到attention中。
一般而言，上下文型的相对位置编码的效果要稍比偏置型的相对位置编码好一些。
可学习的位置编码

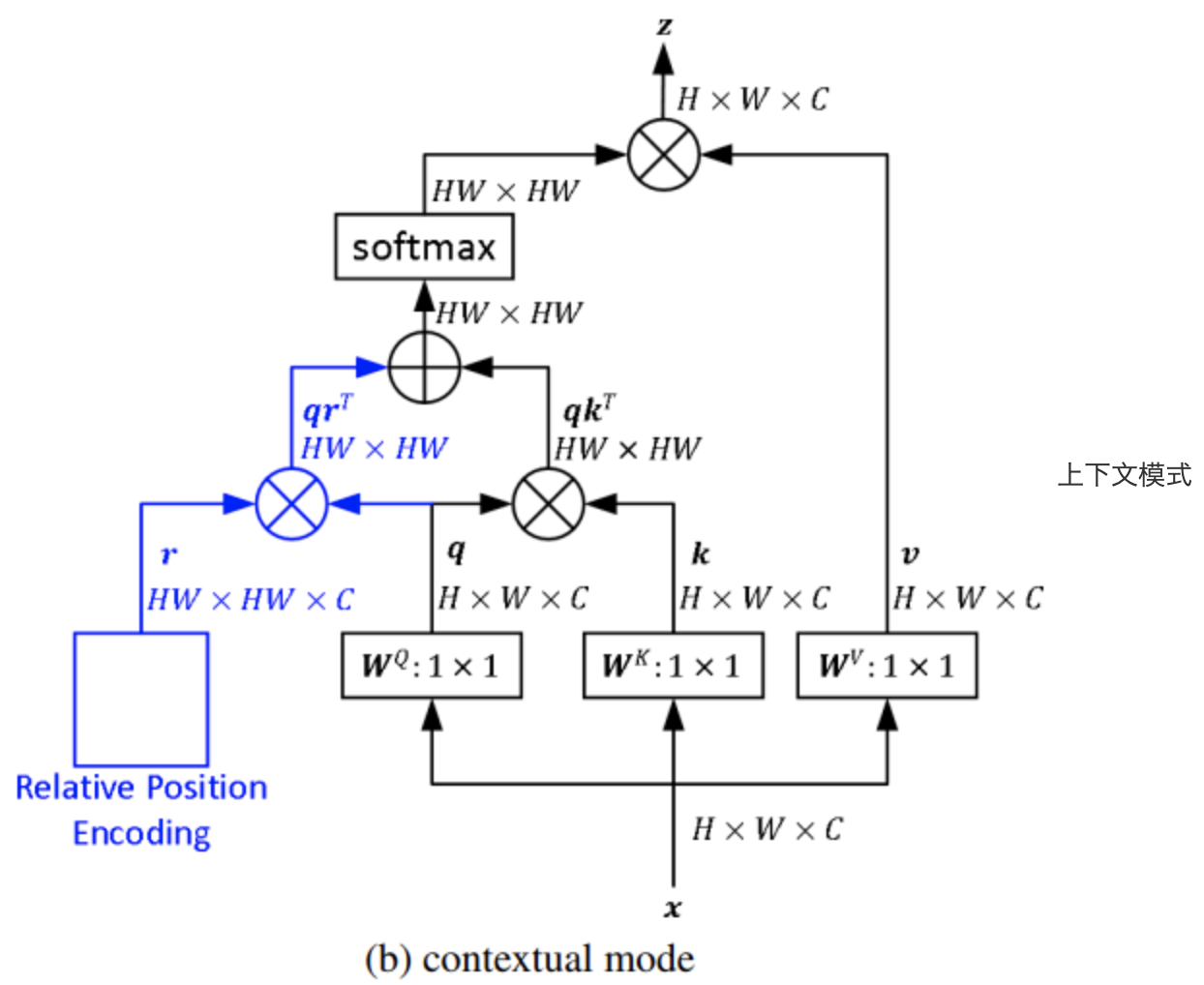
1.3 Encoder侧self-attention计算方式

self attention
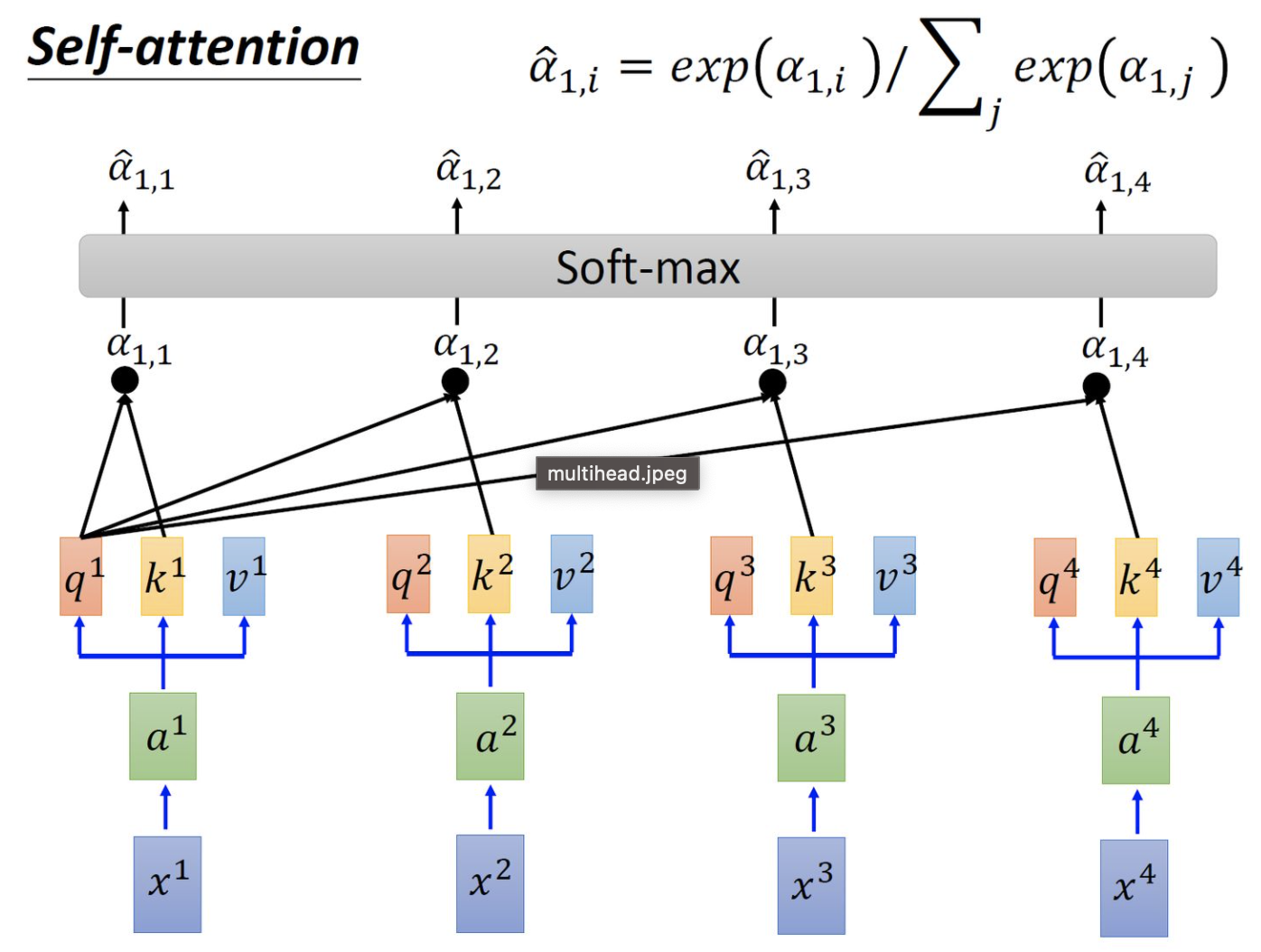
attention乘以value
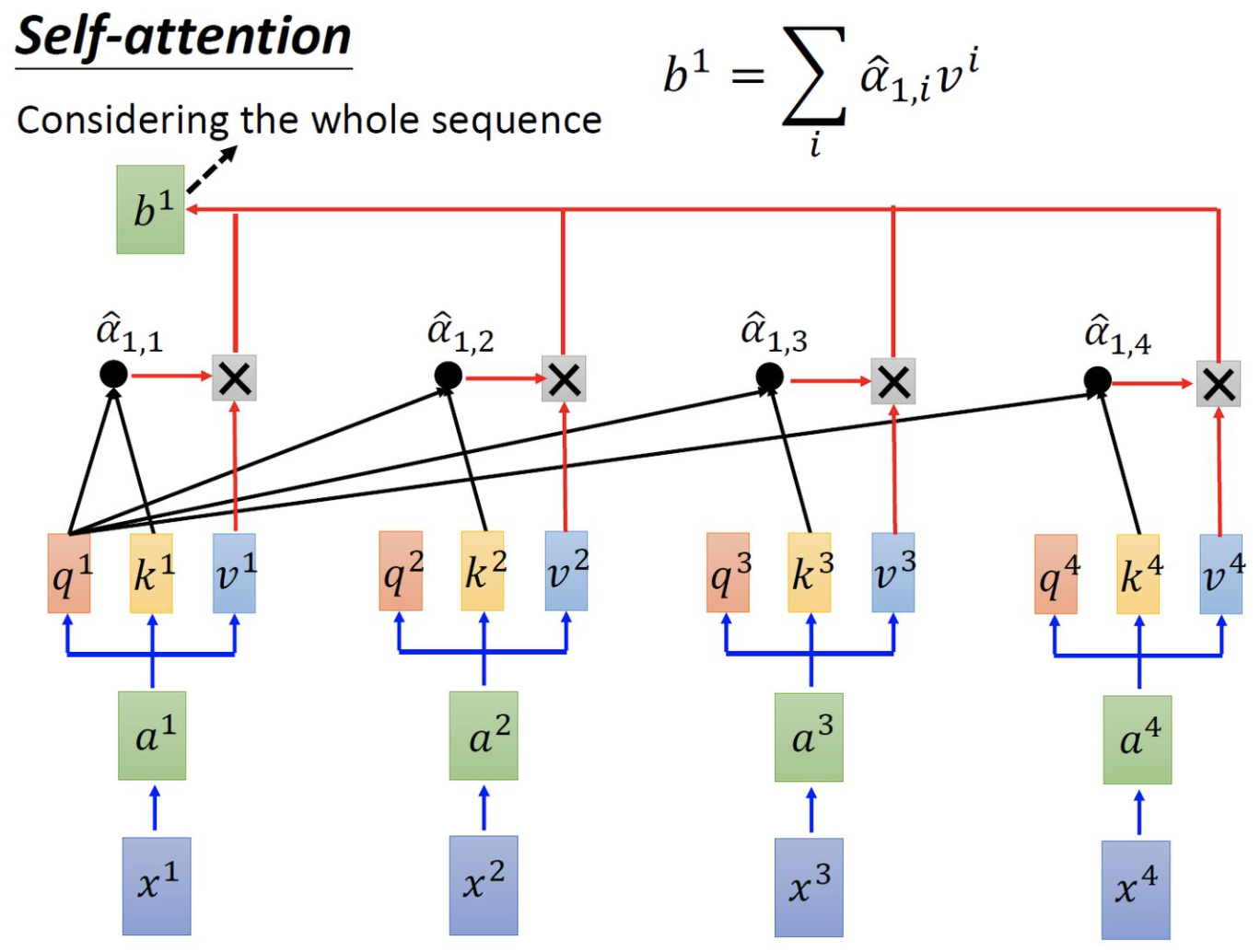
并行计算$b_1, b_2, b_3, b_4$:
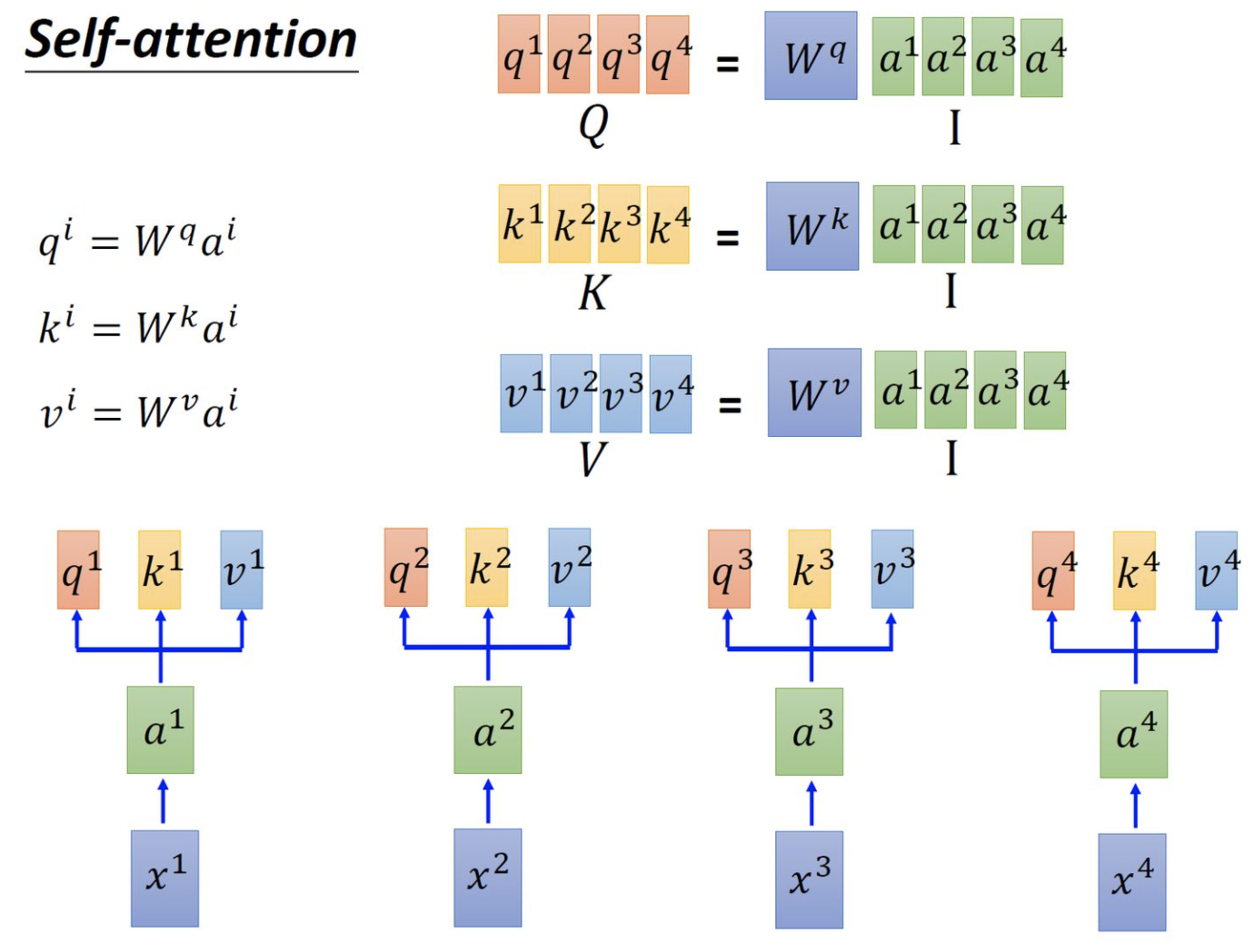
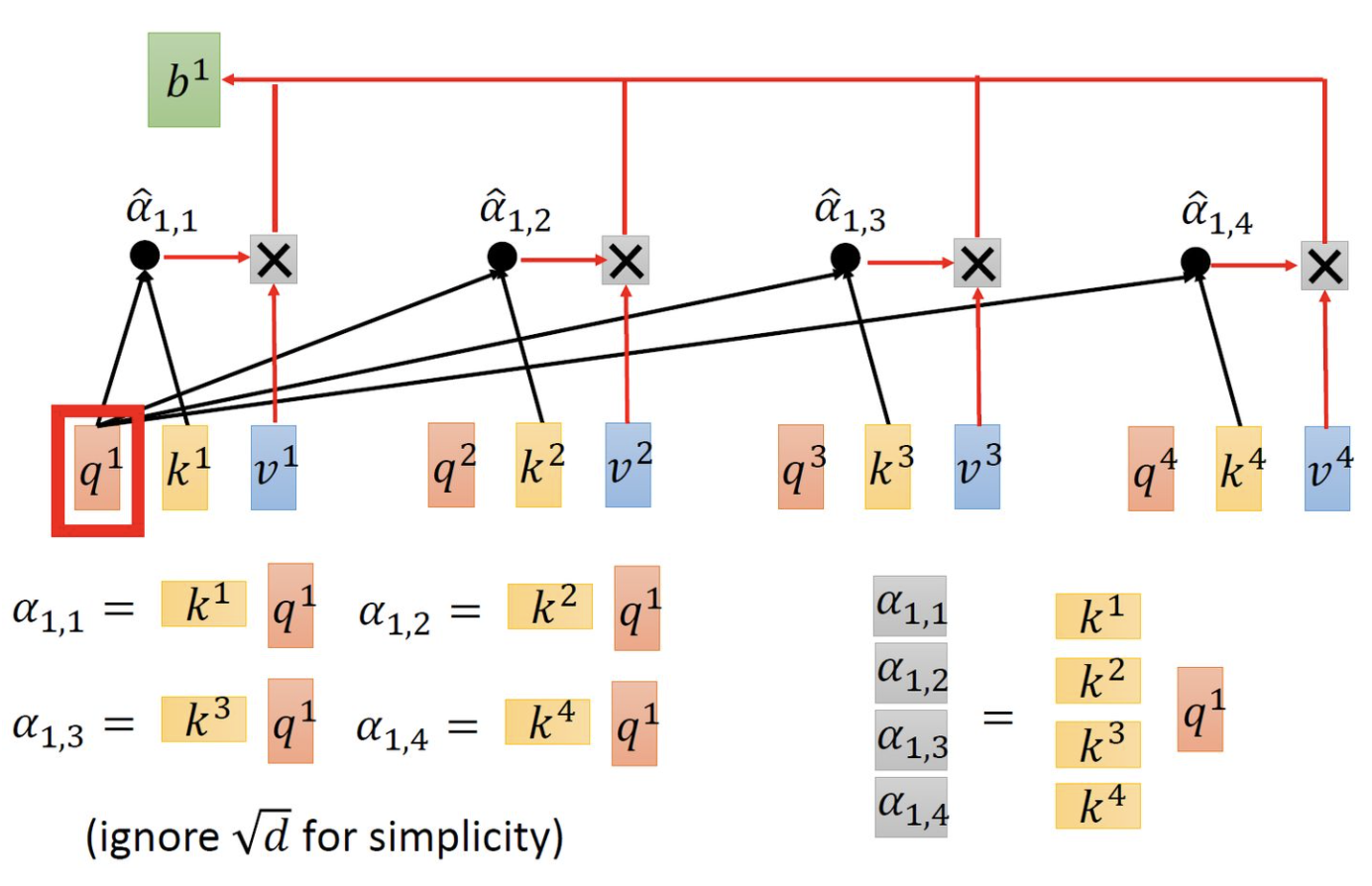
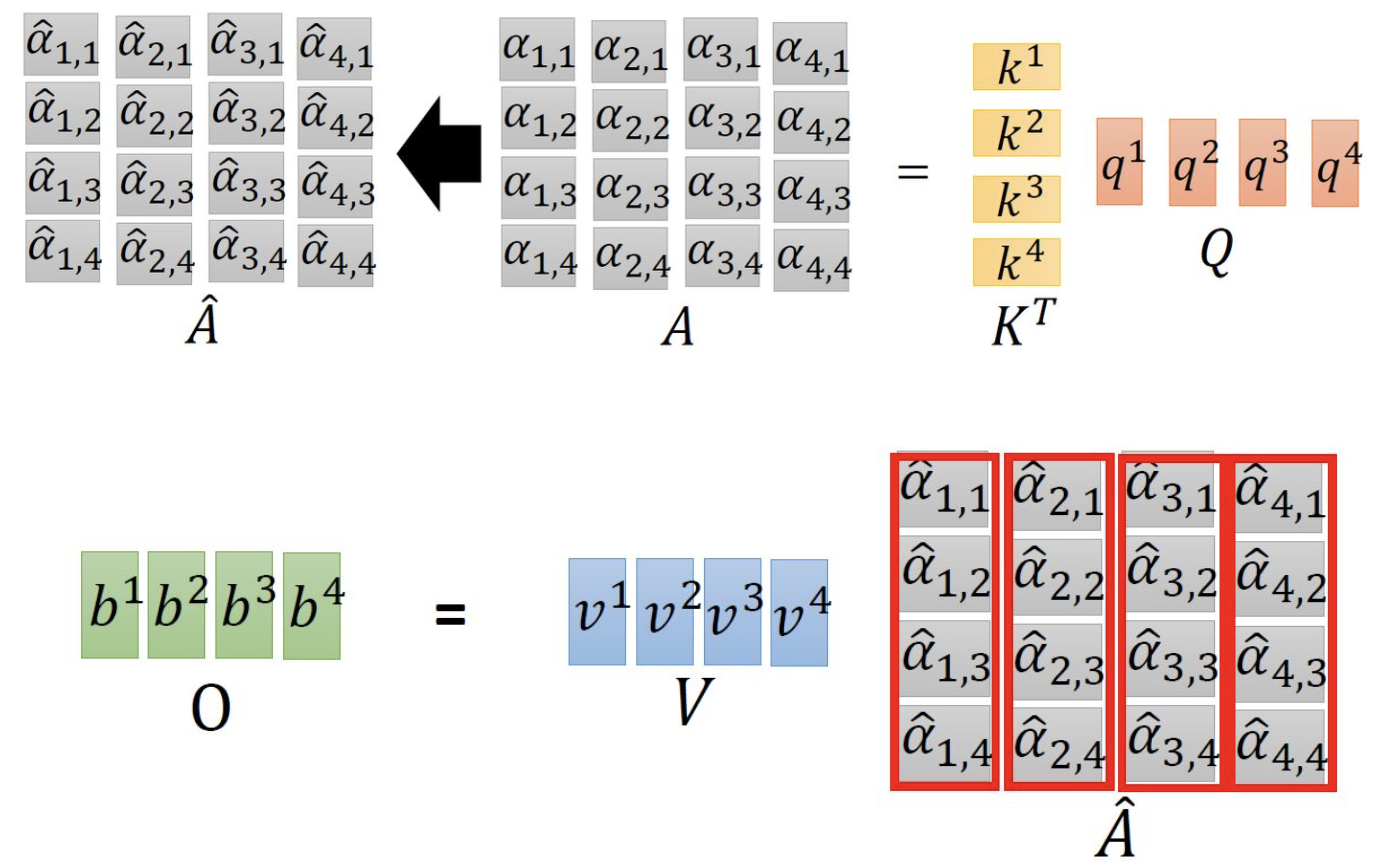
whole process of Encoder layer of Transformer

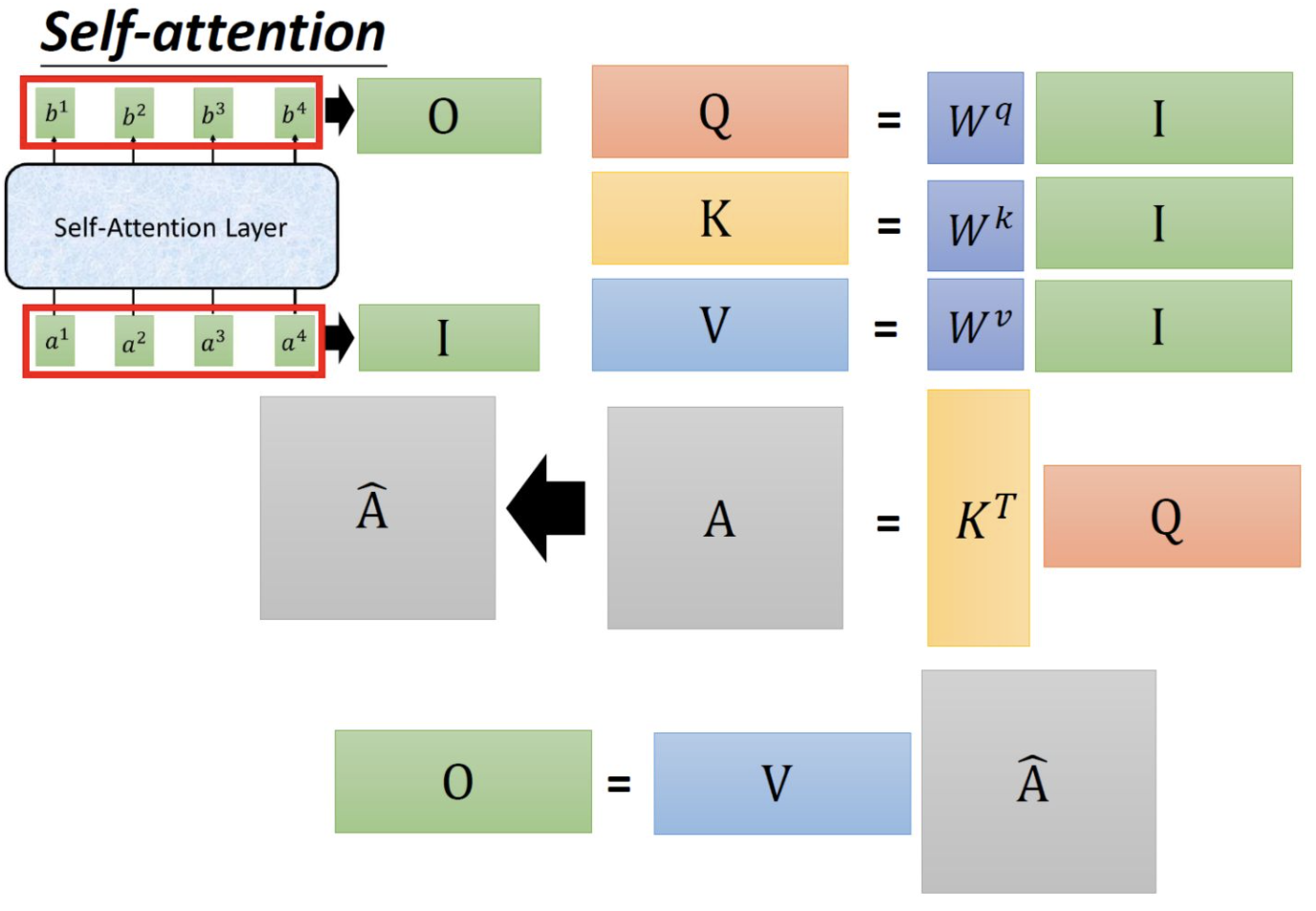
1.4 Decoder侧mask-self-attention计算方式

Decoder侧在训练时，我们的输出侧的序列数据的样例一般是[[start] $x_1, x_2, x_3, x_4, x_5$]，按照和输入侧的attention一样的计算方式，我们可以得到一个$6\times 6$的attention，但是考虑到下文的数据不应该对上文结果预测带来影响，因此，我们要在attention矩阵中添加一个target_mask矩阵，该矩阵是一个下三角矩阵，下三角处为0，上三角处为负的极大值如-100000，然后将target_mask矩阵和计算得到的attention相加，就可以得到真正的，不关注下文信息的attention了，接着进行正常的softmax和ratio_scale，再和value相乘，就得到了最后的输出value。整体的计算思路是先计算，再进行mask掩盖。

1.5 Encoder- Decoder- attention计算方式

在具体实现过程中，我们使用的其实还是和encoder侧相同的self-attention计算函数，只是调用的query, key, value不同了。在计算encoder-decoder-attention时，我们query来自于decoder输出的value值，key和value来自encoder的输出value值，然后进行正常计算就好咯。

1.6 Decoder输出结果接分类头

Decoder的输出value经过了transformer内部的ffn(全连接层)映射，但要进行word的分类时，还需要最后接一个全连接层Linear Layer将ffn层后feature的dimension转换为target_vocab_size，比如target的单词中加上特殊的[start]，[end]，[pad]，[unknown]等token后总共有6023个，那就是要进行6023个类别的分类，经过最后的linearLayer映射后，使用cross Entropy Loss即可以计算损失了。

1.7 Decoder侧mask在训练和测试时的异同

在训练时，我们的Decoder侧的target_mask的size是固定的，因为整个target语言的句子的最大长度我们在训练数据集中能够得到，因此可以直接先使用pad将所有target语言的句子补齐成为一样的长度，然后生成target_mask来掩盖无效的attention。
在测试时，我们的Decoder侧的输序列是随着翻译进度而逐渐增加的，从最开始只有一个[start]的token到后面翻译的target单词越来越多，因此测试时的target_mask是实时根据Decoder侧输入序列数据的长度来变化的。