多视图几何(八)
Chapter8 Direct Approaches to Visual SLAM8.1 Classical Approaches to Multiple View ReconstructionIn the past chapters we have studied classical approaches to multiple view reconstruction. These methods tackle the problem of structure and motion estimation (or visual SLAM) in several steps:
A set of feature points is extracted from the images -ideally points points such as corners which can be reliably identified in subsequent images as well.
One determines a correspondence of these points acros ...
多视图几何(七)
Chapter7 Bundle Adjustment & Nonlinear Optimization7.1 Optimality in Noisy Real World ConditionsIn the previous chapters we discussed linear approaches to solve the structure and motion problem. In particular, the 8-point algorithm provides closed-form solutions to estimate the camera parameters and the 3D structure, based on singular value decomposition. (SVD)
However, if we have noisy data $\tilde{\textbf{x}_1}, \tilde{\textbf{x}_2}$ (correspondence not exact or even incorrect), then we ha ...
多视图几何(六)
Chapter6 Reconstruction from Multiple Views6.1 Multiple View GeometryIn this section, we deal with the problem of 3D reconstruction given multiple views of a static scene, either obtained simultaneously, or sequentially from a moving camera.The key idea is that the three-view scenario allows to obtain more measurements to infer the same number of 3D coordinates. For example, given two views of a single 3D point, we have four measurements (x- and y-coordinate in each view), while the three-view c ...
多视图几何(五)
Chapter5 Reconstruction from Two Views5.1. Problem FormulationIn the last sections, we discussed how to identify point correspondences between two consecutive frames. In this section, we will trackle the next next problem, namely that of reconstructing the 3D geometry of cameras and points.To this end, we will make the following assumptions:
We assume that we are given a set of corresponding points in two frames taken with the same camera from different vantage points.
We assume that the scene ...
多视图几何(四)
Chapter 4 Estimating Point Correspondence4.1 From Photometry to GeometryIn the last sections, we discussed how points and lines are transformed from 3D world coordinates to 2D image and pixel coordinates.
In practice, we do not actually observe points or lines, but rather brightness or color values at the individual pixels. In order to transfer from this photometric representation to a geometric representation of the scene, one can identify points with characteristic image features and try to as ...
多视图几何(三)
Chapter 3 Perspective Projection3.1 Mathematics of Perspective Projection
The perspective transformation $\pi$ from a point with coordinates $\textbf{X}=(X,Y,Z)\in \mathbb{R}^3$ relative to the reference frame centered at the optical center and with z-axis being the optical axis (of the lens) is obtained by comparing similar triangles $\textbf{A}$ and $\textbf{B}$:$$\frac{Y}{Z} = -\frac{y}{f} \Leftrightarrow y = -f\frac{Y}{Z}.$$
To simplify equations, one flips the signs of x- and ...
多视图几何(二)
Chapter 2 Representing a Moving Scene2.0 Overview2.0.1 The Origins of 3D ReconstructionThe goal to reconstrcut the 3D structure of the world from a set of 2-D views has a long history in computer vision. It is a classical ill-posed problem, because the reconstruction consistent with a given set of observations/images is typically not unique. Therefore, one will need to impose additional assumations. Mathematically, the study of geometric relations between a 3D scene and the observed 2D proj ...
MVG-多视图几何(一)
多视图几何(Multi view Geometry)中广泛使用到矩阵运算,因此在开始MVG之旅前,先将MVG中重点使用的线代表示介绍一下。这一章中主要涉及到向量空间的表示以及基本的矩阵运算,包括像内积与叉积。接着有适用于刚体运动的李群和李代数的讲解,最后涉及到特征值,特征向量,以及通过SVD分解求解方程的知识。
Chapter 1 Mathematical Background Linear Algebra##1.1 Vector Spaces
A set $V$ is called a linear space or a vector space over the field $\mathbb{R}$ if it is closed under vector summation$$+:V\times V \rightarrow V$$and under scalar multiplication$$\dot : \mathbb{R} \times V \rightarrow V, $$
i.e. $\alpha v_1 + \beta v_2 \in V \forall v_1, ...
Transformer的前世今生
引言Transformer,用过都说好。Transformer统治了NLP的半壁江山后,已经开始大规模蚕食CV的诸多任务了。这篇文章总结了Transformer的诞生和里面的具体细节,作为自己的总结文章bia :raising_hand:。
1. 机器翻译的发展研究员们为了进行机器翻译,得到你现在使用的Google翻译,百度翻译等等翻译引擎,从1950年就开始了努力。他们尝试过各种各样的方法,比如一大推略显朴素和僵硬的既定规则,或者是设定一些翻译的范例和prototype,又或者使用数据驱动的方式,借助数以万计的翻译数据来设计深度学习模型来进行自动化的翻译。从发展历程来看,我们有了以下这样几种翻译方案:
「基于规则的机器翻译RBMT」
「基于范例的机器翻译EBMT」
「统计机器翻译SMT」
「神经机器翻译NMT」
RBMT,EBMT距离我们太远,就不再细细讲述,我们简短回顾一下SMT方案和NMT方案。
1.1 基于统计的机器翻译典型的SMT模型中有基于短语(phase)的PBMT。基于短语的统计翻译,将基本的翻译单元从原来的整句调整到了短语级别,被切分的短语不一定具有任何语法意义 ...
Vison Transformer系列文章解读(一)
引言x x x
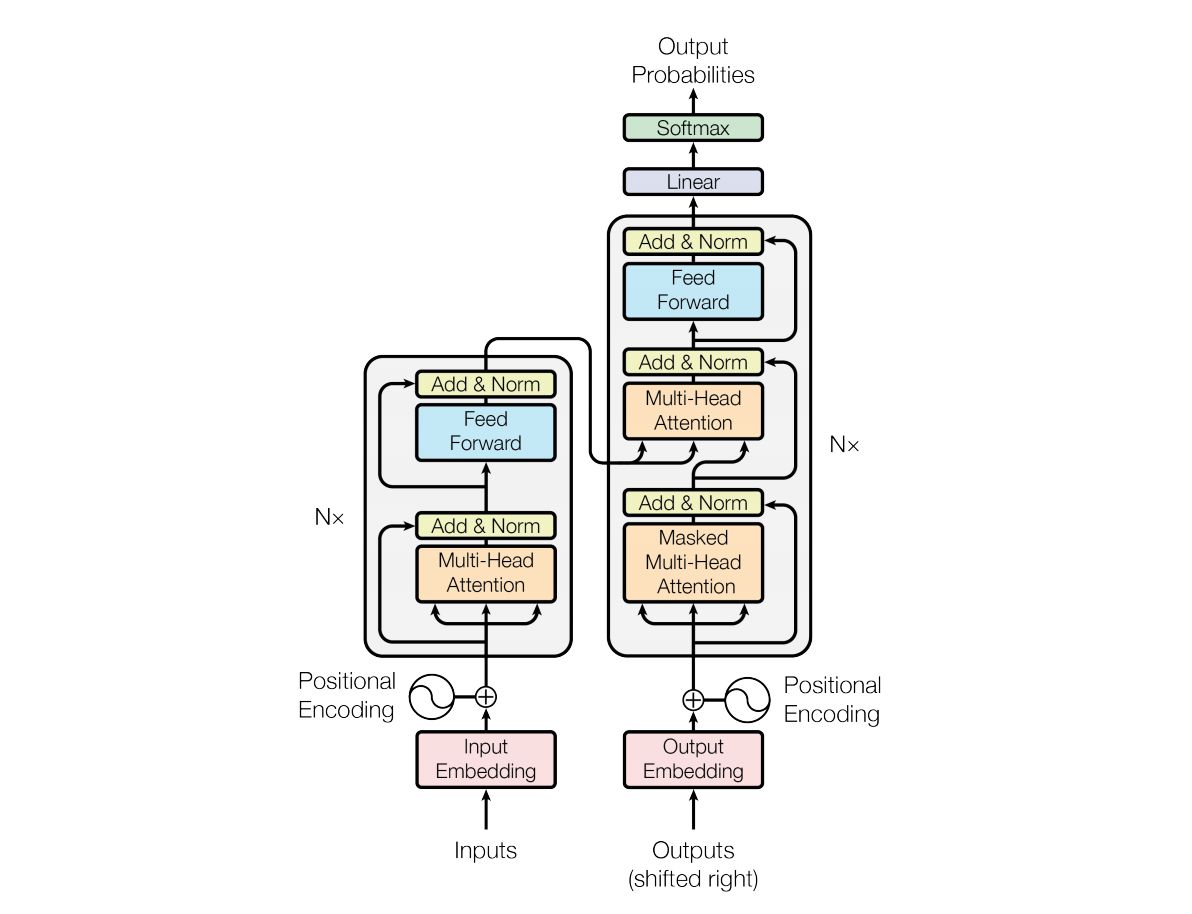
1. Transformer快速回顾我们先来简单而快速的回顾一下Transformer的构成。和串处理数据的Seq2Seq模型不同,Transformer在处理序列数据时,能够做到并行,这也使得Transformer在Seq2Seq模型中快速脱颖而出。
1.1 Encoder侧输入数据详情假设上图中的Encoder侧的inputs是一个[$ x^1, x^2, x^3, x^4$]的序列,该序列长度为4,而每个时间点上的输入数据$ x^i \in \R^{d_{model}}$,这样一个shape为[seq_len, $ d_{model}$]的tensor进入到input Embedding中,通过乘以三种不同的可学习权重矩阵$ W_q, W_k, W_v$,其中$W_q \in \mathbb{R}^{d_{model}\times dimension}, W_k \in \R^{d_{model}\times dimension}, W_v \in \R^{d_{model}\times dimension}$,然后就可以将原来$d_{model}$维的序列数 ...